L'interférométrie holographique électronique
Par l'utilisation de différents algorithmes de déphasage (décalage de phase), on peux obtenir un nombre d'image de speckles (d'habitude 3, 4 ou 5) qui permettent de générer en temps réel et à la cadence vidéo, dans un processeur dédié, des images caractérisées par les mêmes distributions d'intensités que les images reconstruites par les interférogrammes holographiques. Le décalage de phase peut être implémenté, par exemple, à l'aide des actionneurs piézo-électriques intercalés dans le chemin de l'onde de référence ou de l'onde-objet. Un tel dispositif introduit donc une différence de phase supplémentaire entre l'onde-objet et l'onde de référence, noté
L'expression de l'intensité pour une image devient donc:
MESURE DES VIBRATIONS
Dans le cas d'un objet en état de vibration harmonique stationnaire, cette expression devient:
En appliquant, pour quatre images successives,des déphasages
on obtient les expressions:
Le processeur calcule et affiche sur l'écran du moniteur une cinquième image, dont l'expression est
ou, en faisant les calculs:
On reconnaît une expression similaire à celle de l'interférométrie holographique à intégration temporelle; la figure (a) montre un hologramme électronique obtenus à l'aide de cet algorithme. La granularité de l'image est supérieure à celle des images obtenues par interférométrie holographique, mais la compensation réside dans l'obtention en temps réel et dans la possibilité d'obtenir des images de phase, donc qui permettent de mesurer les amplitudes de vibration. Pour réduire le bruit de speckles et le bruit de numérisation on peut faire appel à une addition entre plusieurs images de ce type, avec éventuellement une rotation incrémentale du faisceau d'éclairage. Le bruit est sensiblement réduit, comme illustré dans la figure (b).
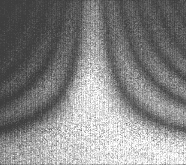
Dans notre laboratoire, on utilise aussi une procédure qui, tout en gardant le caractère "temps réel", assure un profile quasi-binaire des franges en éliminant la fonction de Bessel de l'expression de l'image (et donc un contraste nettement amélioré). Cette procédure assure en même temps une étendue de mesure double et facilite largement l'interprétation quantitative complète. La figure suivante permet de comparer les images holographiques, les profils d'une ligne et les histogrammes pour un même état de vibration (amplitude, fréquence) mesuré par la procédure "classique" (a) et par la procédure mentionnée (b) .
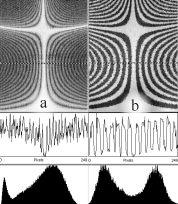
MESURE DES DEFORMATIONS STATIQUES
Des algorithmes semblables à ceux décrits dans le cas de l'étude des
vibrations permettent d'obtenir en temps réel aussi bien des images similaires
à celles obtenues par interférométrie holographique (image à gauche) que la
distribution de phase modulo 2pi (figure centrale). En post-traitement on
obtient la distribution de phase avec recalage de la phase (image à droite)
donc pratiquement la carte des déplacements. C'est l'étape la plus difficile,
qui nécessite l'utilisation d'algorithmes robustes et rapides de recalage de
phase, capables d'éliminer les variations aléatoires rapides de la phase dues
aux speckles.
|
|
|
|
|
|
|
|
|
|
|
|
L'image de phase finale permet, après avoir lui avoir apporté les corrections de perspective et de vecteur de sensibilité comme en interférométrie holographique, d'obtenir les valeurs des déplacements et l'image de la déformée.