La mesure des formes

Techniques de lumière structurée
Mesure des formes 3-D et des grandes déformations


MESURE	RELIEF OBTENU	SURFACE RECONSTRUITE

        Mesurer la forme d'un objet existant présente un grand intérêt, aussi bien en ingénierie que dans d'autres secteurs d'activité (médecine, arts, biens de consommation, contrôle de qualité, topographie, fabrication, etc.).
        En ingénierie mécanique, le problème est actuellement directement lié aux nouvelles technologies de fabrication et à l'utilisation de la CAD. Assez souvent, pour certaines pièces qui doivent être modifiées ou dupliquées, des données de CAD n'existent simplement pas, ou alors elles sont inaccessibles ou insuffisantes. D'autre part, pour les pièces construites à l'aide de la CAD, une comparaison s'impose entre le modèle et sa réalisation physique.
        Mesurer une forme géométrique complexe est une tache très difficilement abordable par les techniques de mesure classiques, s'agissant d'obtenir les coordonnées tri-dimensionnelles d'un grand nombre de points et de les transférer vers un logiciel de CAD.
        Intégrée aujourd'hui au "prototypage rapide" et à la "rétroingénierie" (reverse engineering), la mesure des formes bénéficie de l'apport des techniques optiques globales et des techniques de déphasage inspirées par l'interférométrie et plus particulièrement par l'interféromètrie holographique électronique.

Les méthodes de mesure utilisées au laboratoire de Photomécanique sont basées sur quelques techniques de base, utilisées séparèment ou conjointement: lumière structurée (ex. codes Gray), moiré, projection de franges; elles utilisent des techniques de Fourier et/ou le décalage de phase, associés à la triangulation.

La mesure du relief d'un objet par projection de franges avec décalage de phase

La surface d'un objet tridimensionnel est décrite par une équation du type O(x,y,z) = 0.
Le relief de cet objet est une fonction f(x,y) décrivant l'altitude z du point M de la surface, z = f(x, y) . Afin d'obtenir un nombre de courbes , on éclaire l'objet à l'aide d'un projecteur de franges.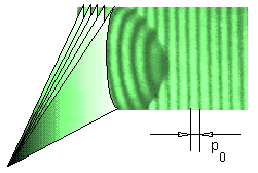

Plusieurs types de projecteurs de franges peuvent être envisagés. Nous utilisons actuellement un interféromètre de type Mach-Zender, pourvu des éléments de réglage nécessaires pour contrôler le nombre de franges et leur inclinaison; dans un plan de référence le pas des franges peut ainsi établi à la valeur désirée.

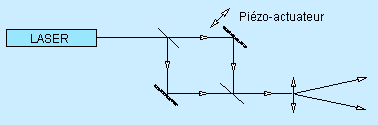
L'un des miroirs de l'interféromètre est prévu d'un piézo-actionneur basse tension, destiné à produire le déphasage spatial du réseau de franges; les déphasages sont controlés avec une résolution de 8 bits par l'une des sorties analogiques de la carte d'acquisition d'images.

Parmi les intérêts de cette solution, on peut citer un bon contraste et une bonne focalisation des franges en tout point du volume du corps mesuré, la disponibilité du laser pour utilisation dans d'autres montages de mesure (holographiques par exemple) ainsi que le caractère modulaire et portable du système.
Une image acquise par la caméra CCD peut être décrite par l'expression:
avec, comme notations:
I(x, y):         l'intensité lumineuse dans le plan de l'image correspondant à un point de l'objet éclairé par les franges;
:     l'intensité lumineuse dans le plan de l'image correspondant à un point de l'objet;
C(x, y):        le contraste local de l'image
:      la phase spatiale correspondant à la position d'un point de l'objet;
a:              phase spatiale supplémentaire introduite à l'aide de l'actionneur piézo- électrique.
    Pour mesurer la phase on procède à l'éclairage successif de l'objet par quatre réseaux déphasés de franges, obtenus en faisant , i = 0, 1, 2, 3. On obtient ainsi les images :

La figure animée présentée au début du document réunit la succession d'images ainsi obtenues.
La phase (modulo2p) est obtenue par la relation: . On peut aussi l'obtenir en utilisant des techniques de transformées Fourier; dans ce cas, le décalage de phase n'est plus nécessaire.

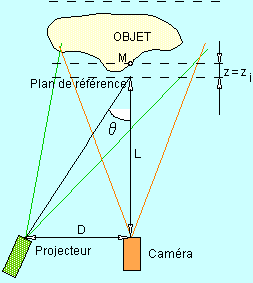
Le montage expérimental utilisé est illustré dans la figure. La caméra CCD et le déphaseur piézo sont controlés par un ordinateur Pentium (PHOTO 3, en salle de TP Photoélasticité du laboratoire de Mesures Expérimentales)
En calculant la différence de phase Dj entre la phase de l'objet et la phase qui correspond au plan de référence indiqué sur la figure, on peut obtenir le relief de l'objet.
Pour le montage illustré, la relation approximative entre cette différence de phase spatiale Dj(x, y) et le relief de l'objet est::

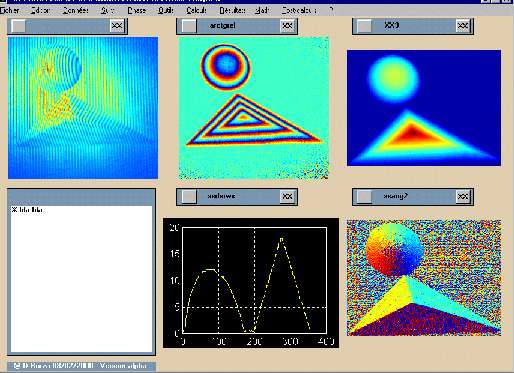
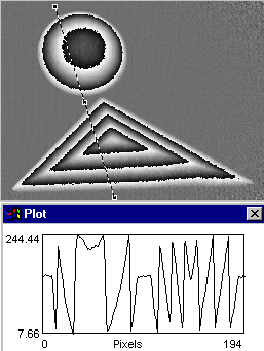
Dans l'exemple qui sera présenté on a enregistré trois séries de 4 images déphasées. Dans la première série d'images, on a simplement projeté les franges sur un plan de référence; dans la deuxième série on a placé sur ce plan de référence une calote sphérique; dans la troisième série, à côté de la calote sphérique on a placé un tétrahèdre. La première image de franges correspondant à chaque série est présentée dans les images suivantes.

Pour chaque série d'images on a ensuite calculé la phase modulo2p conformément à la relation présentée.
L'utilisation de la fonction "arctangente" conduit normalement à des valeurs de la phase (wrapped phase) modulop; la connaissance des signes de sin j et de cos j permet l'obtention des valeurs de modulo2p.

A partir de la distribution de phase modulo2p on obtient, par démodulation à l'intérieur d'une zone d'intérêt rectangulaire, la phase déroulée (unwrapped phase) pour chacune des images de phase modulo2p.


PHASE 1	PHASE 2	PHASE 3

Ensuite, il ne reste qu'à calculer les différences entre deux images de phase. A mentionner que si la première des deux images est l'image du plan de référence, on obtient ainsi le relief (par rapport au plan de référence) de l'objet représenté dans la deuxième image. Si, par contre, les deux images représentent deux scènes différentes et qu'aucune d'elles n'est l'image du plan de référence, on obtient la différence entre les deux scènes, donc les déformations ou les modifications intervenues. Par exemple, dans la troisième image ci-après, on présente la différence entre la phase de l'ensemble tétrahèdre - calote sphérique, d'une part, et la phase de la calote sphérique uniquement, de l'autre part. On obtient ainsi le relief du tétrahèdre.


PHASE 3 - PHASE 1	PHASE 1 - PHASE 2	PHASE 2 - PHASE 3

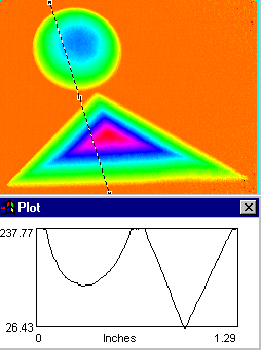
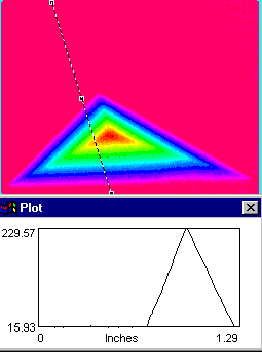
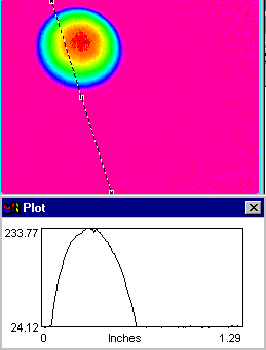
Il existe d'autres algorithmes qui permettent de calculer directement la différence de phase (d'abord modulo2p, ensuite démodulée) entre deux séries d'images, sans avoir à passer par la phase correspondant à chaque série. Ainsi, les deux images suivantes présentent la phase modulo2p et la phase démodulée obtenues directement à partir de la série d'images de l'ensemble calote sphérique - tétrahèdre et de la série d'images du plan de référence. Le profile de la phase le long d'une droite arbitraire illustre l'aspect typique (en dents de scie) pour l'image modulo2p, respectivement la phase démodulée.

Les algorithmes et les programmes pour démoduler les images de phase, basés sur des principes très variés, sont particulièrement sensibles au bruit, surtout au bruit de speckles qui caractérise les images obtenues en lumière cohérente. Une comparaison entre leurs performances et limitations constituera l'objet d'un texte à suivre.


Phase modulo2p	Phase démodulée

Pour les deux autres situations, les différences de phase et les distributions des phases le long de la même droite sont aussi présentées. A mentionner que les images de phase présentées sont des images "brutes", obtenues sans aucun lissage.

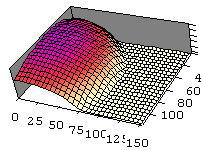
L'obtention des coordonnées tri-dimensionnelles exactes nécessite un étalonnage initial, pour prendre en considération les effêts de perspective du projecteur de franges et de la caméra CCD, ainsi que les caractéristiques géométriques de l'ensemble de mesure. Après avoir effectué cet étalonnage, on peut obtenir le nuage de points en coordonnées x,y,z - ce qui permet d'identifier certaines surfaces définies par ces points - par exemple, les parties planes et sphériques, tel qu'on voit dans la dernière image de la figure suivante.

HOME